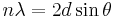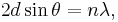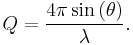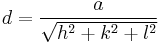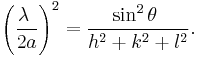Bragg's law
In physics, Bragg's law gives the angles for coherent and incoherent scattering from a crystal lattice. When X-rays are incident on an atom, they make the electronic cloud move as does any electromagnetic wave. The movement of these charges re-radiates waves with the same frequency (blurred slightly due to a variety of effects); this phenomenon is known as Rayleigh scattering (or elastic scattering). The scattered waves can themselves be scattered but this secondary scattering is assumed to be negligible.
A similar process occurs upon scattering neutron waves from the nuclei or by a coherent spin interaction with an unpaired electron. These re-emitted wave fields interfere with each other either constructively or destructively (overlapping waves either add together to produce stronger peaks or subtract from each other to some degree), producing a diffraction pattern on a detector or film. The resulting wave interference pattern is the basis of diffraction analysis. This analysis is called Bragg diffraction.
Bragg diffraction (also referred to as the Bragg formulation of X-ray diffraction) was first proposed by William Lawrence Bragg and William Henry Bragg in 1913 in response to their discovery that crystalline solids produced surprising patterns of reflected X-rays (in contrast to that of, say, a liquid). They found that these crystals, at certain specific wavelengths and incident angles, produced intense peaks of reflected radiation (known as Bragg peaks). The concept of Bragg diffraction applies equally to neutron diffraction and electron diffraction processes.[1] Both neutron and X-ray wavelengths are comparable with inter-atomic distances (~150 pm) and thus are an excellent probe for this length scale.
W. L. Bragg explained this result by modeling the crystal as a set of discrete parallel planes separated by a constant parameter d. It was proposed that the incident X-ray radiation would produce a Bragg peak if their reflections off the various planes interfered constructively. The interference is constructive when the phase shift is a multiple of 2π; this condition can be expressed by Bragg's law,[2]
Where n is an integer, λ is the wavelength of incident wave, d is the spacing between the planes in the atomic lattice, and θ is the angle between the incident ray and the scattering planes. Note that moving particles, including electrons, protons and neutrons, have an associated De Broglie wavelength.
Bragg's Law was derived by physicist Sir William Lawrence Bragg[3] in 1912 and first presented on 11 November 1912 to the Cambridge Philosophical Society. Although simple, Bragg's law confirmed the existence of real particles at the atomic scale, as well as providing a powerful new tool for studying crystals in the form of X-ray and neutron diffraction. William Lawrence Bragg and his father, Sir William Henry Bragg, were awarded the Nobel Prize in physics in 1915 for their work in determining crystal structures beginning with NaCl, ZnS, and diamond. They are the only father-son team to jointly win. W. L. Bragg was 25 years old, making him the youngest Nobel laureate.
Contents |
Bragg condition
Bragg diffraction occurs when electromagnetic radiation or subatomic particle waves with wavelength comparable to atomic spacings are incident upon a crystalline sample, are scattered in a specular fashion by the atoms in the system, and undergo constructive interference in accordance to Bragg's law. For a crystalline solid, the waves are scattered from lattice planes separated by the interplanar distance d. Where the scattered waves interfere constructively, they remain in phase since the path length of each wave is equal to an integer multiple of the wavelength. The path difference between two waves undergoing constructive interference is given by 2dsinθ, where θ is the scattering angle. This leads to Bragg's law, which describes the condition for constructive interference from successive crystallographic planes (h, k, and l, as given in Miller Notation)[4] of the crystalline lattice:
where n is an integer determined by the order given, and λ is the wavelength.[5] A diffraction pattern is obtained by measuring the intensity of scattered waves as a function of scattering angle. Very strong intensities known as Bragg peaks are obtained in the diffraction pattern when scattered waves satisfy the Bragg condition.
Reciprocal space
Although the misleading common opinion reigns that Bragg's law measures atomic distances in real space, it does not. This first statement only seems to be true if it's further elaborated that distances measured during a Bragg experiment are inversely proportional to the distance d in the lattice diagram. Furthermore, the 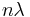 term demonstrates that it measures the number of wavelengths fitting between two rows of atoms, thus measuring reciprocal distances. Reciprocal lattice vectors describe the set of lattice planes as a normal vector to this set with length
term demonstrates that it measures the number of wavelengths fitting between two rows of atoms, thus measuring reciprocal distances. Reciprocal lattice vectors describe the set of lattice planes as a normal vector to this set with length 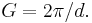 Max von Laue had interpreted this correctly in a vector form, the Laue equation
Max von Laue had interpreted this correctly in a vector form, the Laue equation
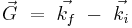
where 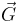 is a reciprocal lattice vector and
is a reciprocal lattice vector and 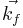 and
and 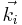 are the wave vectors of the incident and the diffracted beams.
are the wave vectors of the incident and the diffracted beams.
Together with the condition for elastic scattering 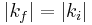 and the introduction of the scattering angle
and the introduction of the scattering angle 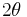 this leads equivalently to Bragg's equation. This is simply explained by the conservation of momentum transfer. In this system the scanning variable can be the length or the direction of the incident or exit wave vectors relating to energy- and angle-dispersive setups. The simple relationship between diffraction angle and Q-space is then:
this leads equivalently to Bragg's equation. This is simply explained by the conservation of momentum transfer. In this system the scanning variable can be the length or the direction of the incident or exit wave vectors relating to energy- and angle-dispersive setups. The simple relationship between diffraction angle and Q-space is then:
The concept of reciprocal lattice is the Fourier space of a crystal lattice and necessary for a full mathematical description of wave mechanics.
Alternate derivation
Suppose that a single monochromatic wave (of any type) is incident on aligned planes of lattice points, with separation  , at angle
, at angle  , as shown below.
, as shown below.
There will be a path difference between the ray that gets reflected along AC' and the ray that gets transmitted, then reflected, along AB and BC respectively. This path difference is
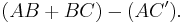
The two separate waves will arrive at a point with the same phase, and hence undergo constructive interference, if and only if this path difference is equal to any integer value of the wavelength, i.e.

(C' needs to be defined)
where the same definition of  and
and  apply as above.
apply as above.
Clearly,
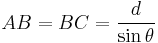 and
and 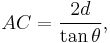
from which it follows that
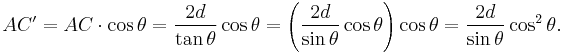
Putting everything together,
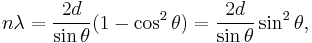
which simplifies to
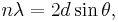
which is Bragg's law.
Bragg scattering of visible light by colloids
A colloidal crystal is a highly ordered array of particles which can be formed over a very long range (from a few millimeters to one centimeter) in length, and which appear analogous to their atomic or molecular counterparts.[6] The periodic arrays of spherical particles make similar arrays of interstitial voids, which act as a natural diffraction grating for visible light waves, especially when the interstitial spacing is of the same order of magnitude as the incident lightwave.[7][8][9]
Thus, it has been known for many years that, due to repulsive Coulombic interactions, electrically charged macromolecules in an aqueous environment can exhibit long-range crystal-like correlations with interparticle separation distances often being considerably greater than the individual particle diameter. In all of these cases in nature, the same brilliant iridescence (or play of colours) can be attributed to the diffraction and constructive interference of visible lightwaves which satisfy Bragg’s law, in a matter analogous to the scattering of X-rays in crystalline solid.
Selection rules and practical crystallography
Bragg's law, as stated above, can be used to obtain the lattice spacing of a particular cubic system through the following relation:
where  is the lattice spacing of the cubic crystal, and
is the lattice spacing of the cubic crystal, and  ,
,  , and
, and 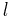 are the Miller indices of the Bragg plane. Combining this relation with Bragg's law:
are the Miller indices of the Bragg plane. Combining this relation with Bragg's law:
One can derive selection rules for the Miller indices for different cubic Bravais lattices; here, selection rules for several will be given as is.
| Bravais lattice | Example compounds | Allowed reflections | Forbidden reflections |
|---|---|---|---|
| Simple cubic | Po, KCl | Any h, k, l | None |
| Body-centered cubic | Fe, W, Ta, Cr | h + k + l even | h + k + l odd |
| Face-centered cubic | Cu, Al, Ni, NaCl, LiH, PbS | h, k, l all odd or all even | h, k, l mixed odd and even |
| Diamond F.C.C. | ZnSe, CuCl, AgI, CuF, Si, Ge | all: odd, or even & h+k+l = 4n | above, or even & h+k+l ≠ 4n |
| Triangular lattice | Ti, Zr, Cd, Be | l even, h + 2k ≠ 3n | h + 2k = 3n for odd l |
These selection rules can be used for any crystal with the given crystal structure. KCl exhibits a fcc cubic structure. However, the K+ and the Cl+ ion have the same number of electrons and are quite close in size, so that the diffraction pattern becomes essentially the same as for a simple cubic structure with half the lattice parameter. Selection rules for other structures can be referenced elsewhere, or derived.
See also
- Crystal lattice
- Diffraction
- Distributed Bragg reflector
- Dynamical theory of diffraction
- Henderson limit
- Laue conditions
- Powder diffraction
- Structure factor
- William Lawrence Bragg
- X-ray crystallography
References
- ^ John M. Cowley (1975) Diffraction physics (North-Holland, Amsterdam) ISBN 0-444-10791-6.
- ^ See, for example, this example calculation of interatomic spacing with Bragg's law.
- ^ There are some sources, like the Academic American Encyclopedia, that attribute the discovery of the law to both W.L Bragg and his father W.H. Bragg, but the official Nobel Prize site and the biographies written about him ("Light Is a Messenger: The Life and Science of William Lawrence Bragg", Graeme K. Hunter, 2004 and “Great Solid State Physicists of the 20th Century", Julio Antonio Gonzalo, Carmen Aragó López) make a clear statement that William Lawrence Bragg alone derived the law.
- ^ H. P. Myers (2002). Introductory Solid State Physics. Taylor & Francis. ISBN 0-7484-0660-3
- ^ Carl. R. Nave. Bragg's Law. HyperPhysics, Georgia State University. http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/bragg.html. Retrieved 2008-07-19
- ^ Pieranski, P (1983). "Colloidal Crystals". Contemporary Physics 24: 25. Bibcode 1983ConPh..24...25P. doi:10.1080/00107518308227471.
- ^ Hiltner, PA; IM Krieger (1969). "Diffraction of Light by Ordered Suspensions". Journal of Physical Chemistry 73: 2306.
- ^ Aksay, IA (1984). "Microstructural Control through Colloidal Consolidation". Proceedings of the American Ceramic Society 9: 94.
- ^ Luck, W. et al., Ber. Busenges Phys. Chem. , Vol. 67, p.84 (1963)
Further reading
- Neil W. Ashcroft and N. David Mermin, Solid State Physics (Harcourt: Orlando, 1976).
- Bragg W.L. (1913). "The Diffraction of Short Electromagnetic Waves by a Crystal". Proceedings of the Cambridge Philosophical Society 17: 43–57.